Verzet, trapfrequentie en crancklengte

Verzet, trapfrequentie en crancklengte zijn populaire onderwerpen in de literatuur en aan de stamtafel in het wielercafé. Welk verzet moet je kiezen om het juiste tempo te rijden zonder dat de benen verzuren? Kies je net als Armstrong voor een koffiemolentje of monteer je de grote molen? Wat is voor jou de optimale trapfrequentie en heeft het zin om een andere lengte van je crancks te monteren? De meeste wielrenners hebben uit ervaring wel ontdekt wat voor hen wel en niet werkt, maar wij willen dit ook theoretisch onderbouwen.

De relatie tussen verzet en snelheid

Dat is het meest fundamentele principe van de moderne fiets. Sinds de uitvinding van de ketting, kunnen we de fietssnelheid vergroten door een groter verzet te monteren. De formule hiervoor is:

V = πDw*TF*nv/na

Als voorbeeld nemen we wieldiameter Dw van 0,71 meter (28 inch), een trapfrequentie TF van 100 rpm (omwentelingen per minuut) en een verzet (dit is de verhouding van het aantal tanden nv vooraan en het aantal tanden na achteraan) van 3, dan wordt de snelheid v 41,29 km/h. In de grafiek is deze relatie weergegeven. Je ziet dat je om een hoge snelheid te halen een flink verzet zult moeten monteren.

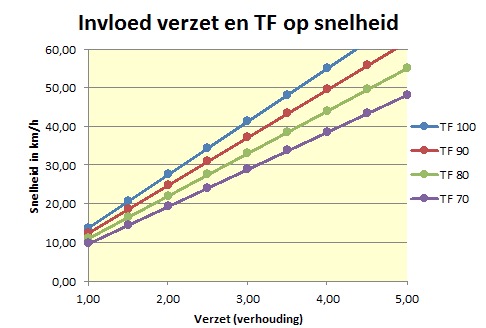De relatie tussen verzet en vermogen

Met een flink verzet kun je weliswaar in theorie een hoge snelheid halen, maar je zult dan een ook in staat moeten zijn om een groot vermogen te trappen. In een vereenvoudigde voorbeeldberekening om de relatie tussen verzet en vermogen goed uit te kunnen leggen gaan er vanuit dat het vermogen alleen bepaald wordt door de luchtweerstand:

Pl = 0,5*ρ*cdA*(v+vw)2*v

Bij de standaardcondities (ρ = 1,205 kg/m3, cdA = 0,3 m2, vw = 0) is een vermogen Pl nodig van 273 Watt om de snelheid van 41,29 km/h te halen. In de bijgaande grafiek zie je dat het vermogen enorm toeneemt met het verzet (net als de snelheid gaat dit tot de 3e macht). Het valt dus niet mee om een groot verzet rond te krijgen.

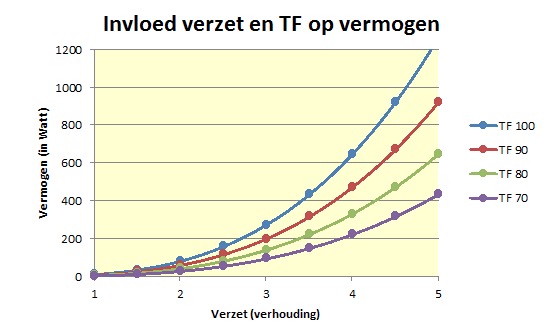De relatie van het verzet met de kracht

Hoe zwaar het ronddraaien van een groot verzet is, kunnen we ook zien aan de trapkracht die nodig als functie van het verzet. Hiervoor geldt de volgende formule:

Ft/Fs = Dw/Dc*nv/na

Als voorbeeld nemen we weer een Dw van 0,71 meter, een diameter van de cranck van 0,35 meter en een verzet van 3. Het resultaat is dan dat je trapkracht Ft ruim 6 keer zo groot moet zijn als de voorstuwingskracht Fs . De Fs wordt in dit voorbeeld alleen gebruikt wordt om de luchtweerstand te overwinnen.

De bijgaande figuur toont hoeveel kracht je nodig hebt om een verzet rond te draaien.

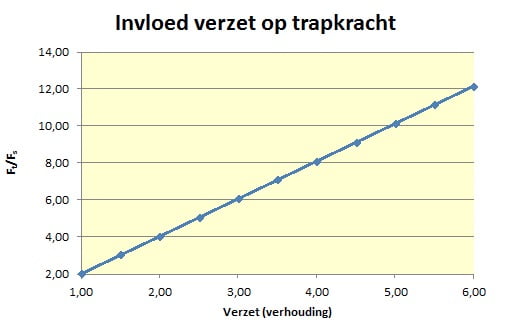
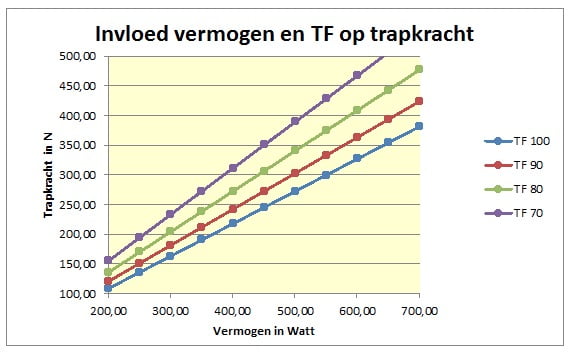
Het is duidelijk dat je trapkracht de beperkende factor is bij het kiezen van het verzet. Dit blijkt nog meer als we de benodigde trapkracht gaan uitdrukken als percentage van je lichaamsgewicht. Dit kunnen we als volgt afleiden:

P = Ft*v

P/mg = Ft/mg* πDw*TF*nv/na

Als voorbeeld nemen we weer een verzet van 3, een TF van 100 en een Dw van 0,71. Dan wordt de benodigde trapkracht (Ft/mg) 6,68% van je lichaamsgewicht bij een specifiek vermogen (P/mg) van 1 Watt/kg. Deze relatie is weergegeven in de bijgaande figuur.

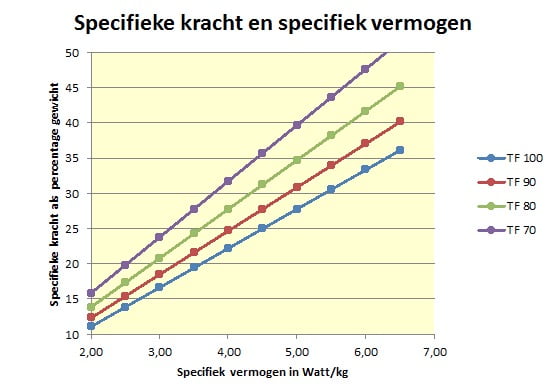
Je ziet dat de wereldtoppers met een specifiek vermogen van 6,4 Watt/kg dus een gemiddelde trapkracht moeten ontwikkelen van 43% van hun lichaamsgewicht. Dit zit heel dicht tegen het maximum van 50% als we bedenken dat je vrijwel alleen kracht kunt zetten tijdens de neergaande cyclus van je trapper.

Wat is nu optimaal?

Uit het bovenstaand kun je al zien dat het lastig is om de optimale keuze te maken voor je verzet en je trapfrequentie. Dit hangt enerzijds sterk af van de gewenste snelheid (en daarmee van de wedstrijdsituatie) en anderzijds van je eigen mogelijkheden qua vermogen en kracht. Veel renners kiezen bij voorkeur een wat lichter verzet en draaien die rond met een hoge frequentie. Op die manier hoeven ze minder kracht te ontwikkelen en sparen ze hun benen. Een TF van 100 op het vlakke en een TF van 70 in de bergen worden vaak gewenst geacht, maar dit kan per renner sterk verschillen.

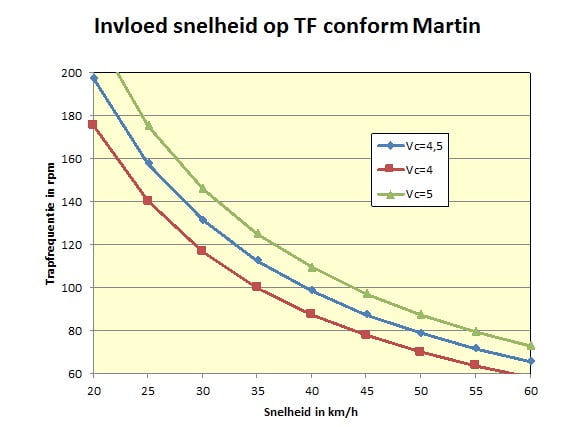
Enige tijd geleden werd een goed onderzoek gepubliceerd naar de optimale trapfrequentie. Hieruit bleek dat niet zozeer de TF zelf geoptimaliseerd dient te worden, maar de cyclische snelheid. Deze is gedefinieerd als het product van de TF en de pedaalsnelheid. Uit het onderzoek bleek dat alle renners een optimaal vermogen trapten als de cyclische snelheid gelijk was aan 4 – 5 (Hz*m/s).

Als we bedenken dat de pedaalsnelheid gelijk is aan de fietssnelheid maal de verhouding van de diameter van het achterwiel en de diameter van de crank, kunnen de volgende vergelijking afleiden:

vc = TF/60*vp = TF/60*v/3,6*(Dw/Dc)

Als we de optimale vc op 4,5 (Hz*m/s) stellen, de TF op 100, de snelheid v op 40 km/h, en de Dw op 0,71 m, kunnen we berekenen dat de optimale Dc dan 0,17 meter wordt. Dit is uiteraard een veelgebruikte crancklengte. Uit de vergelijking kunnen we wel afleiden dat de bij toenemende snelheid de optimale trapfrequentie moet afnemen, zie de figuur (gebaseerd op Dw = 0,71 en Dc = 0,175).

Je kunt het effect van alle aspecten op je eigen prestaties berekenen met onze calculators op www.hetgeheimvanwielrennen.nl. Daar kun je ook ons boek bestellen. Het is ook verkrijgbaar als ebook.

Hans van Dijk, Ron van Megen en Guido Vroemen