Fmv = m*v2/R
Evenwichtshoek in de bochtJe kunt dit opvangen door in de bocht wat schuin te gaan hangen. Hierdoor zorg je voor een evenwicht tussen Fmv en de horizontale component van de zwaartekracht Fg:Fmv = Fg*tg(φ)
Omdat Fg gelijk is aan m*g, komen we tenslotte tot :tg(φ) = v2/(g*R)
Als voorbeeld geldt bij v = 40 km/h en R = 20 meter, tg(φ) = 0,63, dus de evenwichtshoek φ is 32°.De figuur geeft de invloed van de snelheid en de kromtestraal op de evenwichtshoek. Je ziet dat bij hoge snelheden en kleine kromtestralen je heel schuin moet hellen om niet uit de bocht te vliegen.Om bij zo’n helling niet te vallen, moet de evenwichtshoek in de praktijk kleiner blijven dan 45 0 en bij een nat wegdek zelfs kleiner dan 35°. Dat betekent dat je bij krappe bochten zult moeten afremmen, zeker bij een nat wegdek.
Evenwichtssnelheid op een wielerbaanOp een wielerbaan zijn de bochten aangelegd onder een schuine hoek β. Dat betekent dat er precies evenwicht is als φ gelijk is aan β. Als we dit invullen in de vergelijking van de middelpuntvliedende kracht, is het resultaat:ve = √(g*R*tg(β))
Als voorbeeld nemen we β = 45° en R = 20 meter, dan is de evenwichtssnelheid ve gelijk aan 50,5 km/h. Als je langzamer rijdt dan is het risico aanwezig dat je naar beneden slipt, als je sneller rijdt is het risico aanwezig dat je omhoog glijdt. De figuur toont de evenwichtssnelheid als functie van β en R.
Wat is het effect van de verhoogde g-waarde in de bochten?In de bochten ondervindt je een kracht die gelijk is aan de resultante van de zwaartekracht en de middelpuntvliedende kracht. Dit betekent dat je in feite blootgesteld worden aan een verhoogde g-waarde:gv = √(1+(v2/g*R)2)
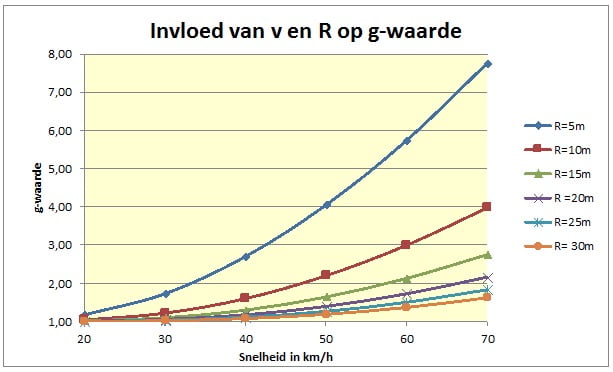
Als voorbeeld nemen we weer een v van 40 km/h en een R van 20 meter, dan is de gv-waarde 1,18. Met andere woorden: je wordt blootgesteld aan een g-waarde die 1,18 keer groter is dan de zwaartekracht. In de figuur zie je dat de g-waarde met name flink kan toenemen bij hoge snelheden en krappe bochten.
We hebben hier ook een berekening over gemaakt bij de aanval van Thomas Dekker op het werelduurrecord in Mexico op 25 februari 2015. De baan daar heeft een R van 21 m en Thomas reed met een snelheid van 52 km/h, zodat hij in de bochten een g-waarde ondervond van 1,44 keer de zwaartekracht. Omdat de beide bochten een lengte hebben van 132 meter en de totale lengte van de baan 250 meter is, betekent dit dat zijn rolweerstand gemiddeld een factor 1,23 groter was dan normaal.Dit kostte Thomas 5 Watt extra vermogen. Dit lijkt weinig, maar is toch 1,5% van het totale vermogen van 367 Watt dat Thomas tijdens zijn recordpoging trapte. In dit opzicht was het beter geweest als de baan wat ruimer geweest was met een grotere lengte en ruimere bochten.Hoeveel invloed hebben bochten in een proloog?Een bochtig parcours kan bij een korte proloog een behoorlijke invloed hebben op de snelheid en de berekeningen met onze calculator. Als voorbeeld nemen we een proloog van 10 km met in totaal 5 scherpe bochten. We stellen dat de kromtestraal van de bochten zo klein is dat de renners gedwongen zijn om af te remmen tot 30 km/h (5,55 m/s). We nemen verder aan dat ze 25 meter voor de bocht remmen en 25 meter na de bocht weer de kruisnelheid van 52 km/h (14,44 m/s) bereikt hebben. Zonder de bocht zouden ze die 50 meter afgelegd hebben in 50/14,44 = 3,5 seconden, met de bocht duurt het 50/5,55 = 9 seconden. In totaal kosten de bochten dus 5*(9-3,5) = 27,5 seconden. Met een kruissnelheid van 52 km/h, legt de renner een parcours zonder bochten af in 10000/14,44 = 692,5 seconden. Met bochten doet hij er 720 seconden over. Zijn tijd neemt dus met bijna 4% toe en zijn gemiddelde snelheid neemt 4% af. Dit heeft een grote invloed als we bedenken dat een 4% hogere snelheid overeenkomt met een 12% groter vermogen! Fabian Cancellara legde bijvoorbeeld de proloog van de Tirreno Adriatico in 2015 af met een gemiddelde snelheid van 53,26 km/h. Als we dit invoeren in onze calculator (m = 81 kg+6,8 kg fiets, cdA = 0,25, cr = 0,003, hoogte 23 m, temperatuur 20 °C) dan is het resultaat dat hij 545Watt aan vermogen heeft getrapt. Als we rekenen met een 4% hogere snelheid, dan heeft hij 610 Watt aan vermogen moeten trappen! Het laatste lijkt ons reëler, hoewel we het parcours niet precies kennen. De 610 Watt komt overeen met een specifiek vermogen van 7,5 Watt/kg en een ADV van 6,3 Watt/kg (gerekend met een piekfactor van 1,19 omdat de inspanningsduur maar 6 minuten was). Dit lijken reële waarden voor een wereldtopper als Cancellara is.Je kunt het effect van alle aspecten op je eigen prestaties berekenen met onze calculators op www.hetgeheimvanwielrennen.nl. Daar kun je ook ons boek bestellen. Het is ook verkrijgbaar als ebook.Hans van Dijk, Ron van Megen en Guido Vroemen