Tot nu toe hebben we alle berekeningen uitgevoerd voor de evenwichtssituatie. Dat wil zeggen dat het vermogen van de renner gelijk is aan de som van de rolweerstand, de luchtweerstand, de klimweerstand en de mechanische weerstand. Dit evenwicht leidt ertoe dat de snelheid constant blijft.
Bij demarrages en de eindsprint is dit natuurlijk niet het geval. De renner mobiliseert in korte tijd een hele grote trapkracht en een heel groot vermogen, waardoor de snelheid flink toeneemt. In feite kun je stellen dat de versnelling die dan optreedt bepaald wordt door het verschil van de trapkracht en de kracht die nodig is om de rolweerstand en de luchtweerstand te overwinnen:
m*a = Ft– Fr–Fl
Als voorbeeld nemen we Ft = 114 N, Fr = 2 N, Fl = 33 N en m = 83,8 kg, dan wordt de versnelling a gelijk aan 0,97 m/s2. In 1 seconde neemt de snelheid dan dus met 3,5 km/h toe. Zo’n grote kracht kan de renner uiteraard maar enkele seconden volhouden, dus zijn jump moet precies juist getimed zijn om het verschil te kunnen maken.
Voorbeeld van een eindsprint
Ter illustratie hebben we een voorbeeld uitgewerkt. We hebben weer de standaardcondities genomen (ρ = 1,205 kg/m3, cdA = 0,3 m2, cr = 0,004, m = 75 kg+8,8 kg fiets) en gesteld dat de renner in een peloton rijdt dat met 60 km/h aan het sprinten is. In het peloton heeft onze renner een 40% lagere luchtweerstand. Dat voordeel van de lagere luchtweerstand raakt hij kwijt als hij alleen op kop komt. Met onze calculator kun je dan berekenen dat het benodigd vermogen van onze renner 543 Watt is als hij nog in het peloton rijdt. We hebben vervolgens gesteld dat onze renner een topsprinter is met een maximaal vermogen (gedurende 5 seconden) van 6 Watt/kg*75 kg*4,23 (piekfactor) = 1903 Watt.
Het verschil tussen het piekvermogen van 1903 Watt en het basisvermogen van 543 Watt gaat nu leiden tot een versnelling die we kunnen berekenen met:
a = (Pp-Pb)/v*m
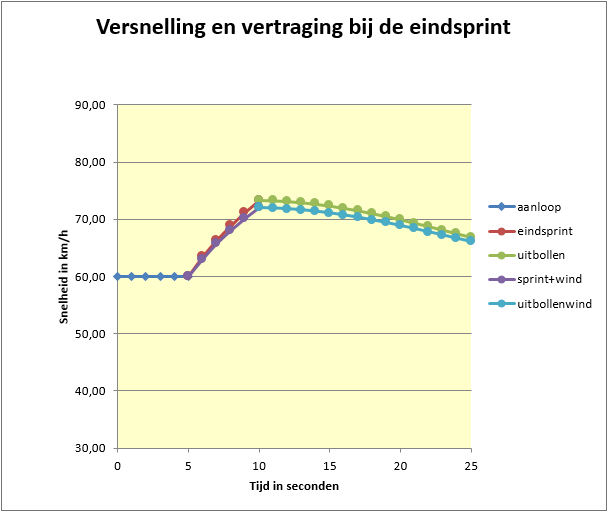
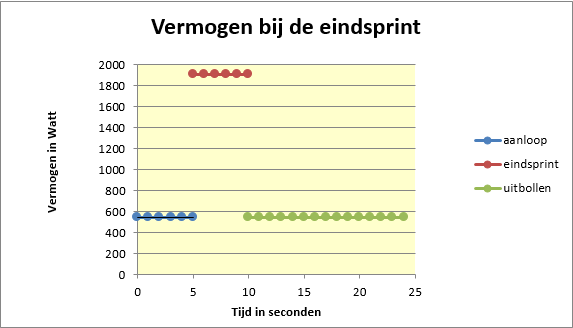
In ons voorbeeld met v = 60 km/h, m = 83,8 kg en de genoemde vermogens, wordt a inderdaad 0,97 m/s2, want we hebben hetzelfde voorbeeld gebruikt. In de bijgaande grafieken zie je vervolgens hoe de snelheid en het vermogen zich in de eindsprint ontwikkelen. De renner kan het vermogen maximaal 5 seconden volhouden, waarna hij noodgedwongen gaar uitbollen. Zijn snelheid daalt dan weer langzaam naar de basissnelheid. We hebben in de figuur tevens het effect aangegeven van het ‘in de wind komen’ van de sprinter, als hij op kop komt. Hij raakt het voordeel van de luwte van het peloton dan kwijt, waardoor zijn cdA-waarde stijgt en zijn maximale snelheid maar 72,0 km/h wordt i.p.v. 73,38 km/h.
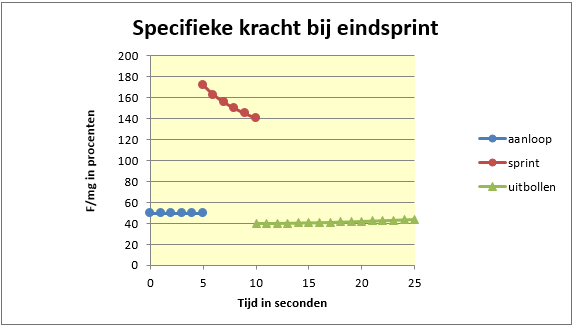
Tenslotte hebben we nog de specifieke kracht berekend van de sprinter als percentage van zijn lichaamsgewicht. In de grafiek zie je dat hij maximaal maar liefst 179% van zijn lichaamsgewicht moet kunnen trappen!
 De invloed van het traagheidsmoment van de wielen
De invloed van het traagheidsmoment van de wielen
Strikt genomen moeten we in de bovenstaande formules niet rekenen met de som van het gewicht van de renner en het gewicht van de fiets (in ons voorbeeld dus 75+8,8 kg = 83,8 kg), maar moeten we daar het traagheidsmoment van de wielen nog bij optellen. In de praktijk is dit een kleine factor, het massatraagheidsmoment van de wielen ligt in de orde van 2 kg, zodat we eigenlijk hadden moeten rekenen met 85,8 kg. Dit betekent dat je versnelling iets minder wordt, in de orde van 2% minder. Voor het voorbeeld maakt dat niet uit. Voor een sprinter die in de praktijk kan kiezen voor wielen met een wat kleiner traagheidsmoment kan dit natuurlijk wel een mooi voordeeltje opleveren!
Je kunt het effect van alle aspecten op je eigen prestaties berekenen met onze calculators op
www.hetgeheimvanwielrennen.nl. Daar kun je ook ons boek bestellen. Het is ook verkrijgbaar als ebook.
Hans van Dijk, Ron van Megen en Guido Vroemen
www.hetgeheimvanwielrennen.nl